Per S. Schmidt and Kristian S. Thygesen
The Journal of Physical Chemistry C Article ASAP
This database contains the adsorption energies of 200 reactions involving 8 different adsorbates on 25 different transition metal surfaces at full coverage as well as the surface energies for the same surfaces. Various DFT functionals have been employed and compared to the results from many-body perturbation theory within the random phase approximation.
The adsorption reactions are
\(\mathrm{H}_2\mathrm{O} + \mathrm{slab} \rightarrow \mathrm{OH/slab} + \frac{1}{2} \mathrm{H}_2\)
\(\mathrm{CH}_4 + \mathrm{slab} \rightarrow \mathrm{CH/slab} + \frac{3}{2} \mathrm{H}_2\)
\(\mathrm{NO} + \mathrm{slab} \rightarrow \mathrm{NO/slab}\)
\(\mathrm{CO} + \mathrm{slab} \rightarrow \mathrm{CO/slab}\)
\(\mathrm{N}_2 + \mathrm{slab} \rightarrow \mathrm{N_2/slab}\)
\(\frac{1}{2}\mathrm{N}_2 + \mathrm{slab} \rightarrow \mathrm{N/slab}\)
\(\frac{1}{2}\mathrm{O}_2 + \mathrm{slab} \rightarrow \mathrm{O/slab}\)
\(\frac{1}{2}\mathrm{H}_2 + \mathrm{slab} \rightarrow \mathrm{H/slab}\)
and the surfaces include 3d transition metals from Scandium (Sc) to Zink (Zn), 4d from Yttrium (Y) to Cadmium (Cd) excluding Technetium (Tc) and 5d from Hafnium (Hf) to Gold (Au).
Per S. Schmidt and Kristian S. Thygesen
The Journal of Physical Chemistry C Article ASAP
The data can be obtained from the files:
Download raw data adsorption.db and surfaces.db
And browsed online:
The adsorption energy is defined with respect to the adsorbate in its gas phase: \(E_{\text{ads}} = E_{\text{adsorbate@slab}} - (E_{\text{slab}} + E_{\text{adsorbate(g)}})\)
And the surface energy as: \(E_{\text{surf}} = \frac12 \bigg( E_{\text{slab}} - N_{\text{layers}} E_{\text{bulk}}\bigg)\), where the number of atomic layers in the slab is \(N_{\text{layers}} = 3\).
One example reaction that the adsorption energy is calculated for is:
\(\mathrm{CH}_4\mathrm{(g)} + \mathrm{Sc} \rightarrow \mathrm{CH/Sc} + \frac32 \mathrm{H}_2\mathrm{(g)}\)
In the database the adsorbate is then \(\mathrm{CH}\), the surface material is \(\mathrm{Sc}\), reference molecule 1 is \(\mathrm{CH}_4\) and reference molecule 2 is \(\mathrm{H}_2\). The adsorption energy is then \(E_{\text{ads}} = E_{\mathrm{CH/Sc}} -(E_{\mathrm{Sc}} + E_{\mathrm{CH}_4\mathrm{(g)}} - \frac32 E_{\mathrm{H}_2\mathrm{(g)}})\).
key |
description |
unit |
|---|---|---|
|
Surface Material |
|
|
Adsorbate |
|
|
Reference molecule 1 |
|
|
Reference molecule 2 |
|
|
Adsorption energy with LDA |
eV |
|
Adsorption energy with PBE |
eV |
|
Adsorption energy with RPBE |
eV |
|
Adsorption energy with BEEF-vdW |
eV |
|
Adsorption energy with vdW-DF2 |
eV |
|
Adsorption energy with mBEEF |
eV |
|
Adsorption energy with mBEEF-vdW |
eV |
|
Adsorption energy with EXX |
eV |
|
RPA correlation adsorption energy extrapolated |
eV |
In the following script it is shown how to extract and plot adsorption and surface energies from the database files (adsorption.db, surfaces.db):
# creates: database_example.svg
import numpy as np
import matplotlib.pyplot as plt
import ase.db
adsorbate = 'NO'
slabs = ['Sc', 'Ti', 'Cu', 'Pd']
db = ase.db.connect('adsorption.db')
db_surf = ase.db.connect('surfaces.db')
labels = ['LDA', 'PBE', 'RPBE', 'BEEF-vdW', 'RPA']
markers = ['o', 's', 'v', 'D', 'x']
markersize = [10, 10, 10, 10, 12]
mews = [1, 1, 1, 1, 4]
cols = ['r', 'k', 'b', 'g']
plt.figure()
for ii, slab in enumerate(slabs):
rows = db.select(adsorbate=adsorbate)
adss = []
for row in rows:
if row.symbols[0] == slab:
adss.append(row.LDA_adsorp)
adss.append(row.PBE_adsorp)
adss.append(row.RPBE_adsorp)
adss.append(row.BEEFvdW_adsorp)
adss.append(row.RPA_EXX_adsorp)
rows_surf = db_surf.select(surf_mat=slab)
surfs = []
for row in rows_surf:
surfs.append(row.LDA_surf)
surfs.append(row.PBE_surf)
surfs.append(row.RPBE_surf)
surfs.append(row.BEEFvdW_surf)
surfs.append(row.RPA_EXX_surf)
for i in range(len(adss)):
if ii == 0:
plt.plot(surfs[i], adss[i], color='darkgray',
marker=markers[i], markersize=markersize[i],
mew=mews[i], label=labels[i])
plt.plot(surfs[i], adss[i], color=cols[ii],
marker=markers[i], markersize=markersize[i], mew=mews[i])
p = np.polyfit(surfs[:-1],
adss[:-1],
deg=1)
plt.plot([surfs[2], surfs[0]],
p[0] * np.array([surfs[2], surfs[0]]) + p[1],
color=cols[ii])
plt.annotate(slabs[ii], (surfs[-1] + 0.02, adss[-1]), color=cols[ii],
size=14)
plt.legend(loc='lower left', numpoints=1, prop={'size': 14})
plt.title('NO adsorption', size=18)
plt.ylim([-3.5, 0])
plt.xlim([0.3, 1.1])
plt.xlabel(r'$E_{\sigma}$ (eV)', size=22)
plt.ylabel(r'$E_{\mathrm{ads}}$ (eV)', size=22)
plt.xticks(size=18)
plt.yticks(size=18)
plt.tight_layout()
plt.savefig('database_example.svg', dpi=500)
Which should generate the following figure showing the adsorption versus surface energy for NO adsorption on four different transition metals:
The surfaces were modeled using three layers with the bottom two layers fixed at the fcc PBE lattice constants from materialsproject.org and the position of the top layer relaxed. The position of the adsorbate was relaxed keeping all three surface layers fixed at the position found previously. All relaxations were carried out with the BFGS algorithm using the PBE approximation to the xc-functional with a force convergence criteria of 0.05 eV/Å. The electron temperature was 0.01 eV and spin-polarized calculations were performed for calculations involving Fe, Ni or Co. 5 Å of vacuum was added to either side of the adsorbate to avoid artificial interactions between neighboring layers following convergence tests at both the DFT and RPA level. The adsorption energies are relative to the molecule in its gas phase and the calculations for the isolated molecules were carried out in a \(6\times6\times6\) Å \(^3\) box fully relaxing the geometry with the PBE functional.
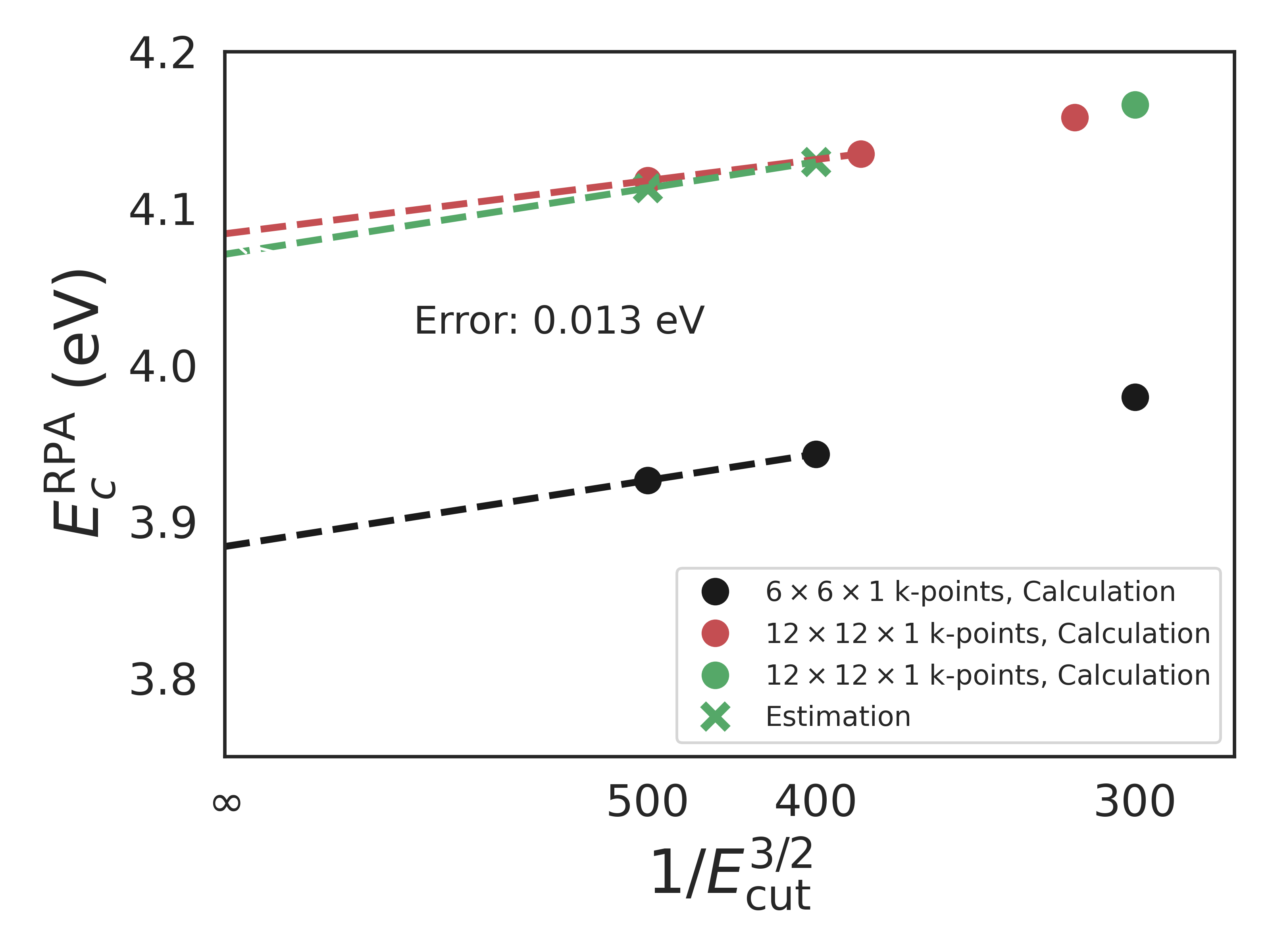
The RPA calculations were carefully converged with respect to plane wave basis using the following extrapolation scheme: In the following figure, the black dots are from a calculation with \(6\times6\times1\) k-points (not enough to achieve convergence) but high cutoff energies (300, 400, 500 eV). The green circle is a calculation at a much denser k-point sampling of \(12\times12\times1\) (converged). From these four circles, the two green crosses are predicted which allow for an extrapolation to infinite cutoff energy. The red dots represent actual calculations with both a dense k-point grid and high cutoff energies to test the extrapolation scheme. The error introduced by the extrapolation scheme for this particular system is seen to be 0.013 eV. The k-point grid of \(12\times12\times1\) ensures that the exchange + correlation energy is converged to within 0.02 eV with respect to the k-point density.