Castelli, I. E., Landis, D. D., Thygesen, K. S., Dahl, S., Chorkendorff, I., Jaramillo, T. F., and Jacobsen, K. W.
Energy Environ. Sci. 5, 9034.
We perform computational screening of around 19 000 oxides, oxynitrides, oxysulfides, oxyfluorides, and oxyfluoronitrides in the cubic perovskite structure with photoelectrochemical cell applications in mind.
Castelli, I. E., Landis, D. D., Thygesen, K. S., Dahl, S., Chorkendorff, I., Jaramillo, T. F., and Jacobsen, K. W.
Energy Environ. Sci. 5, 9034.
Castelli, I. E., Olsen, T., Datta, S., Landis, D. D., Dahl, S., Thygesen, K. S., and Jacobsen, K. W.
Computational screening of perovskite metal oxides for optimal solar light capture.
Energy Environ. Sci. 5, 5814.
Castelli, I. E., Thygesen, K. S., and Jacobsen, K. W.
Calculated Pourbaix Diagrams of Cubic Perovskites for Water Splitting: Stability Against Corrosion.
Topics in Catalysis 57, 265.
key |
description |
unit |
|---|---|---|
|
A-ion in the cubic perovskite |
|
|
B-ion in the cubic perovskite |
|
|
Anion combination in the perovskite |
|
|
Direct bandgap GLLB-SC |
eV |
|
Indirect bandgap GLLB-SC |
eV |
|
Heat of formation |
eV |
|
General formula |
|
|
Direct position of the conduction band edge |
|
|
Indirect position of the conduction band edge |
|
|
Direct position of the valence band edge |
|
|
Indirect position of the valence band edge |
|
|
Reference |
|
|
Standard energy |
from __future__ import print_function
import ase.db
from ase.phasediagram import PhaseDiagram
con = ase.db.connect('cubic_perovskites.db')
references = [(row.formula, row.energy)
for row in con.select('reference')]
with open('abo3.csv', 'w') as fd:
print('# id, formula, heat of formation [eV/atom]', file=fd)
for row in con.select(combination='ABO3'):
pd = PhaseDiagram(references, filter=row.formula, verbose=False)
energy = pd.decompose(row.formula)[0]
heat = (row.energy - energy) / row.natoms
if (heat < 0.21 and
(3.1 > row.gllbsc_ind_gap > 1.4 or
3.1 > row.gllbsc_dir_gap > 1.4) and
(row.VB_ind - 4.5 > 1.23 and row.CB_ind - 4.5 < 0 or
row.VB_dir - 4.5 > 1.23 and row.CB_dir - 4.5 < 0)):
formula = row.A_ion + row.B_ion + row.anion
print('{0}, {1}, {2:.3f}'.format(row.id, formula, heat), file=fd)
The 10 candidates are:
# id |
formula |
heat of formation [eV/atom] |
|---|---|---|
14300 |
SrSnO3 |
0.020 |
14363 |
CaSnO3 |
0.164 |
14410 |
LiVO3 |
0.171 |
14425 |
CsNbO3 |
0.176 |
14688 |
BaSnO3 |
-0.084 |
14863 |
AgNbO3 |
0.207 |
14981 |
SnTiO3 |
0.103 |
15088 |
NaSbO3 |
0.205 |
15292 |
SrGeO3 |
0.157 |
15621 |
CaGeO3 |
0.158 |
Here are the band gaps:
import matplotlib.pyplot as plt
import ase.db
con = ase.db.connect('cubic_perovskites.db')
rows = []
for i, line in enumerate(open('abo3.csv')):
if line[0] == '#':
continue
id, formula = line.split(',')[:2]
id = int(id)
row = con.get(id)
rows.append(row)
plt.text(i - 1.25, -1.9, formula, rotation=60)
N = len(rows)
assert N == 10
x = range(N)
y = [(row.VB_ind + row.CB_ind) / 2 - 4.5 for row in rows]
dyd = [row.gllbsc_dir_gap / 2 for row in rows]
dyi = [row.gllbsc_ind_gap / 2 for row in rows]
plt.errorbar(x, y, dyd, color='k', lw=0, mew=2, elinewidth=2,
label='Direct Gap')
plt.errorbar(x, y, dyi, color='r', lw=0, mew=2, elinewidth=2,
label='Indirect Gap')
plt.xlim(-1, N)
plt.ylim(4.4, -2.2)
plt.axhline(y=0, xmin=-1, xmax=N, lw=2, color='b', ls='dashed')
plt.axhline(y=1.23, xmin=-1, xmax=N, lw=2, color='g', ls='dotted')
plt.text(N + 0.1, 0.2, 'H$^+$/H$_2$', color='b')
plt.text(N + 0.1, 1.43, 'O$_2$/H$_2$O', color='g')
plt.ylabel('Potential (V vs NHE) [eV]')
plt.xticks([-1], '')
plt.legend(loc=4)
plt.savefig('abo3.svg')
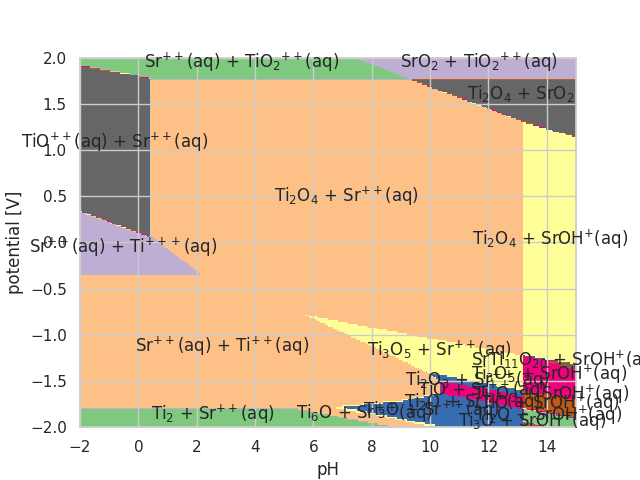
The stability of a material with respect to solid and dissolved phases can be evaluated using Pourbaix diagrams. Here how to generate the Pourbaix diagram for SrTiO3:
# creates: SrTiO3_pourbaix.png
import numpy as np
import matplotlib.pyplot as plt
import ase.db
from ase.phasediagram import Pourbaix, solvated
con = ase.db.connect('cubic_perovskites.db')
refs = []
for row in con.select('reference'):
refs.append((row.formula, row.standard_energy))
# Add other solid/dissolved phases not included before:
refs += [('Ti6O', -5.443), ('Ti2O3', -13.907), ('Ti2O', -5.164),
('TiO', -4.838), ('SrO2', -5.356), ('Ti3O', -5.346),
('Ti3O5', -22.917), ('Sr4Ti3O10', -50.756), ('SrTi11O20', -93.313)]
# Extract the dissolved phases:
refs += solvated('SrTi')
pb = Pourbaix(refs, formula='SrTiO3')
U = np.linspace(-2, 2, 200)
pH = np.linspace(-2, 15, 300)
d, names, text = pb.diagram(U, pH, plot=True, show=False)
plt.savefig('SrTiO3_pourbaix.png')
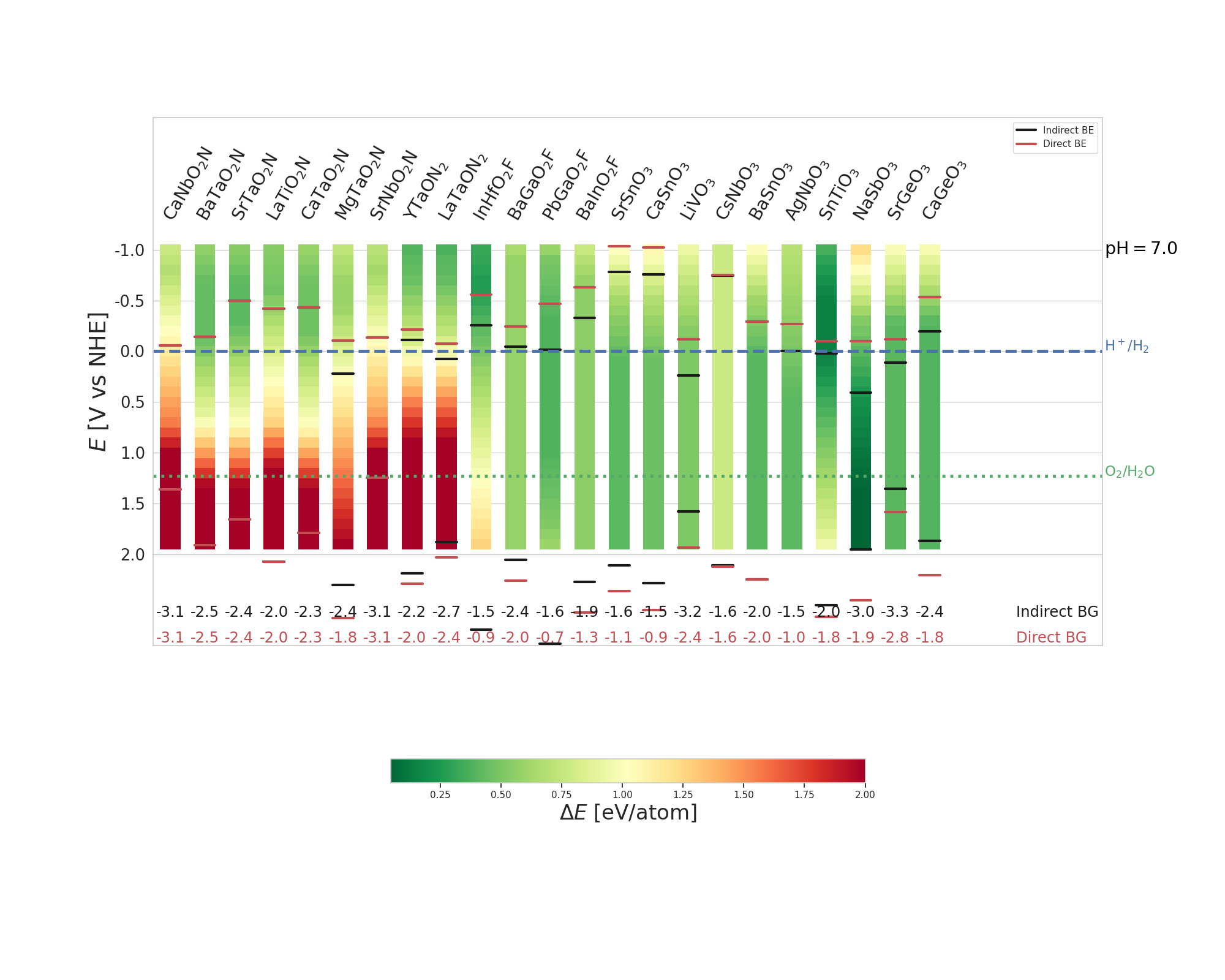
Here how to plot the energy differences for all (oxides: 10, oxynitrides: 7, oxyfluorides: 3) the candidate material and the most stable experimental known solid and dissolved phases at pH = 7 and for a potential between -1 and 2 V:
# creates: WS_pourbaix.png
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from matplotlib.collections import PatchCollection
import matplotlib.patches as patches
import ase.db
from ase.phasediagram import Pourbaix, solvated
con = ase.db.connect('cubic_perovskites.db')
pH = 7.
Us = np.arange(-1, 2, 0.1)
E0 = -4.5
lb = -0.5 # lower bound for the energy scale
ub = 2.0 # upper bound for the energy scale
info = []
xs = []
ys = []
heats = []
for row in con.select('heat_of_formation_all<=0.21'):
if (row.gllbsc_ind_gap >= 1.4 and row.gllbsc_ind_gap <= 3.1 and
row.CB_ind <= 0 - E0 and row.VB_ind >= 1.23 - E0) or \
(row.gllbsc_dir_gap >= 1.4 and row.gllbsc_dir_gap <= 3.1 and
row.CB_dir <= 0 - E0 and row.VB_dir >= 1.23 - E0):
name = row.A_ion + row.B_ion + row.anion
energy = row.standard_energy
info.append([name, row.gllbsc_ind_gap + E0, row.gllbsc_dir_gap + E0,
row.VB_ind + E0, row.CB_ind + E0,
row.VB_dir + E0, row.CB_dir + E0])
refs = []
for row_ref in con.select('reference'):
refs.append((row_ref.formula, row_ref.standard_energy))
# Extract the dissolved phases:
refs += solvated(row.A_ion + row.B_ion)
for U in Us:
pb = Pourbaix(refs, name)
results, refs_energy = pb.decompose(U, pH, verbose=False)
Ediff = (energy - refs_energy) / 5
Ediff = min(Ediff, ub)
Ediff = max(Ediff, lb)
xs.append(len(info) - 1)
ys.append(U)
heats.append(Ediff)
fig = plt.figure(figsize=(20, 16))
ax = fig.add_subplot(111)
cx = 0.3
cy = 0.05
rects = []
for i in range(len(heats)):
rect = patches.Rectangle((xs[i] - cx, ys[i] - cy), 2 * cx, 2 * cy)
rects.append(rect)
p = PatchCollection(rects, edgecolors=None, linewidths=0, cmap=cm.RdYlGn_r)
p.set_array(np.array(heats))
ax.add_collection(p)
for i in range(len(info)):
plt.plot([i - cx, i + cx], [info[i][3], info[i][3]], '-',
color='k', linewidth=3)
plt.plot([i - cx, i + cx], [info[i][4], info[i][4]], '-',
color='k', linewidth=3)
plt.plot([i - cx, i + cx], [info[i][5], info[i][5]], '-',
color='r', linewidth=3)
plt.plot([i - cx, i + cx], [info[i][6], info[i][6]], '-',
color='r', linewidth=3)
plt.text(i, 2.5, round(info[i][1], 1), color='k', fontsize=17.5,
verticalalignment='top', horizontalalignment='center')
plt.text(i, 2.75, round(info[i][2], 1), color='r', fontsize=17.5,
verticalalignment='top', horizontalalignment='center')
plt.plot([cx, cx], [info[0][3], info[0][3]], '-', color='k', linewidth=3,
label='Indirect BE')
plt.plot([cx, cx], [info[0][5], info[0][5]], '-', color='r', linewidth=3,
label='Direct BE')
plt.text(len(info) + 1.5, 2.5, 'Indirect BG', color='k', fontsize=17.5,
verticalalignment='top', horizontalalignment='left')
plt.text(len(info) + 1.5, 2.75, 'Direct BG', color='r', fontsize=17.5,
verticalalignment='top', horizontalalignment='left')
for i in range(len(info)):
formula = info[i][0]
for j in range(10):
if str(j) in formula:
formula = formula.replace(str(j), "$_" + str(j) + "$")
plt.text(i - cx, -1.25, formula, rotation=60, va='bottom', ha='left',
fontsize=20.5, color='k')
xmax = len(info) + 4
plt.text(xmax + 0.05, -1, 'pH$=' + str(pH) + '$', color='black', fontsize=20.5,
verticalalignment='center')
plt.axhline(1.23, xmin=0, xmax=xmax, color='g', ls='dotted', lw=3.5)
plt.text(xmax + 0.05, 1.23, 'O$_2$/H$_2$O', color='g', fontsize=16.5)
plt.axhline(0, xmin=0, xmax=xmax, color='b', ls='dashed', lw=3.5)
plt.text(xmax + 0.05, 0, 'H$^+$/H$_2$', color='b', fontsize=16.5)
cbar = plt.colorbar(p, orientation='horizontal', shrink=0.5)
cbar.set_label(r'$\Delta E$ [eV/atom]', fontsize=24.5)
plt.ylabel('$E$ [V vs NHE]', fontsize=26.5)
plt.yticks([-1, -0.5, 0, 0.5, 1, 1.5, 2],
['-1.0', '-0.5', '0.0', '0.5', '1.0', '1.5', '2.0'],
fontsize=18.5)
plt.xticks([])
plt.legend()
plt.xlim(xmin=-0.5, xmax=xmax)
plt.ylim(ymin=-2.3, ymax=2.9)
plt.gca().invert_yaxis()
plt.savefig('WS_pourbaix.png')