Definition of a scoring parameter to identify low-dimensional materials components

Peter Mahler Larsen, Mohnish Pandey, Mikkel Strange, and Karsten W. Jacobsen

Definition of a scoring parameter to identify low-dimensional materials components

Phys. Rev. Materials 3 034003, 2019

The data can be downloaded or browsed online:

• Download data: lowdim.db

• Browse data

Brief description

The analyses of two databases are available here: the Inorganic Crystal Structure Database (ICSD) and the Crystallography Open Database (COD). The COD database contains the full structures, dimensionality scores, and publication information, for every structure with at most 200 atoms. For copyright reasons, the atomic positions of the ICSD entries cannot be shown here; only the formulae, ICSD code, and dimensionality scores are shown.

Key-value pairs

key	description	unit
s_0	0D score
s_1	1D score
s_2	2D score
s_3	3D score
s_01	0D+1D score
s_02	0D+2D score
s_03	0D+3D score
s_12	1D+2D score
s_13	1D+3D score
s_23	2D+3D score
s_012	0D+1D+2D score
s_013	0D+1D+3D score
s_023	0D+2D+3D score
s_123	1D+2D+3D score
s_0123	0D+1D+2D+3D score
a_0	Start of 0D k-interval
a_1	Start of 1D k-interval
a_2	Start of 2D k-interval
a_3	Start of 3D k-interval
a_01	Start of 0D+1D k-interval
a_02	Start of 0D+2D k-interval
a_03	Start of 0D+3D k-interval
a_12	Start of 1D+2D k-interval
a_13	Start of 1D+3D k-interval
a_23	Start of 2D+3D k-interval
a_012	Start of 0D+1D+2D k-interval
a_013	Start of 0D+1D+3D k-interval
a_023	Start of 0D+2D+3D k-interval
a_123	Start of 1D+2D+3D k-interval
a_0123	Start of 0D+1D+2D+3D k-interval
b_0	End of 0D k-interval
b_1	End of 1D k-interval
b_2	End of 2D k-interval
b_3	End of 3D k-interval
b_01	End of 0D+1D k-interval
b_02	End of 0D+2D k-interval
b_03	End of 0D+3D k-interval
b_12	End of 1D+2D k-interval
b_13	End of 1D+3D k-interval
b_23	End of 2D+3D k-interval
b_012	End of 0D+1D+2D k-interval
b_013	End of 0D+1D+3D k-interval
b_023	End of 0D+2D+3D k-interval
b_123	End of 1D+2D+3D k-interval
b_0123	End of 0D+1D+2D+3D k-interval
numc_0	Number of 0D components
numc_1	Number of 1D components
numc_2	Number of 2D components
numc_3	Number of 3D components
source	Source
dbid	ID #
doi	DOI
publication	Publication
spacegroup_number	Space group #
dimtype	Dimensionality
h	Component count
warning	Warning

Example

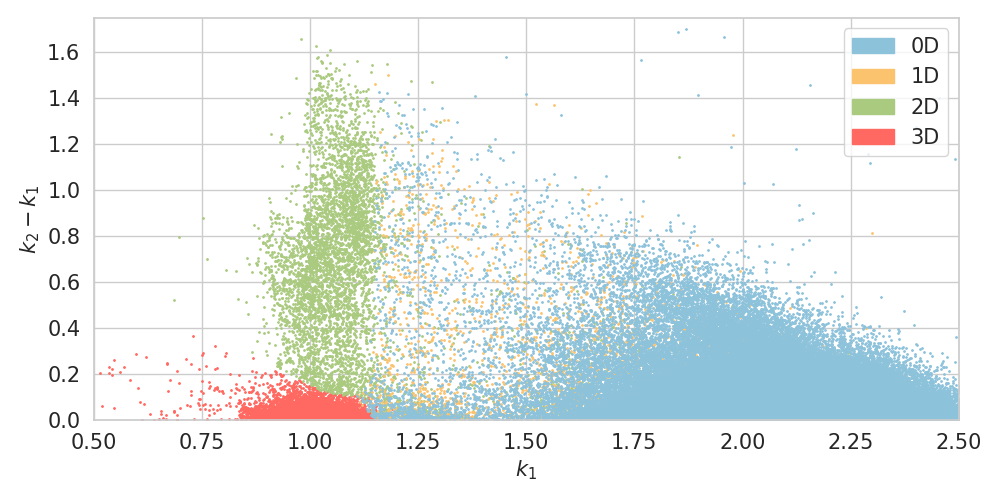
# creates: lowdim.png
import numpy as np
from ase.db import connect
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.patches import Patch

fontsize = 15
matplotlib.rcParams['xtick.labelsize'] = fontsize
matplotlib.rcParams['ytick.labelsize'] = fontsize


def run_example():
    c = connect('lowdim.db')
    rows = [r for r in c.select()]

    dims = [0, 1, 2, 3]
    colors = ['#8dc2db', '#fbc36e', '#aaca7f', '#ff6961']

    data = []
    for row in rows:
        if 'a_2' in row and 'b_2' in row:
            k1 = row.a_2
            k2 = row.b_2
            dim = int(row.dimtype[:-1])
            if dim in dims:
                data.append((k1, k2 - k1, dim))
    data = np.array(data)

    plt.figure(figsize=(10, 5))
    for dim in dims[::-1]:
        indices = np.where(data[:, 2] == dim)[0]
        xs = data[indices, 0]
        ws = data[indices, 1]
        plt.scatter(xs, ws, c=colors[dim], s=1)

    patches = [Patch(color=colors[dim], label="%dD" % dim) for dim in dims]
    plt.legend(handles=patches, loc='upper right', fontsize=fontsize)

    plt.xlim(0.5, 2.5)
    plt.ylim(0, 1.75)
    plt.xlabel(r'$k_1$', fontsize=fontsize)
    plt.ylabel(r'$k_2 - k_1$', fontsize=fontsize)

    plt.tight_layout()
    plt.savefig('lowdim.png')
    plt.close()


run_example()